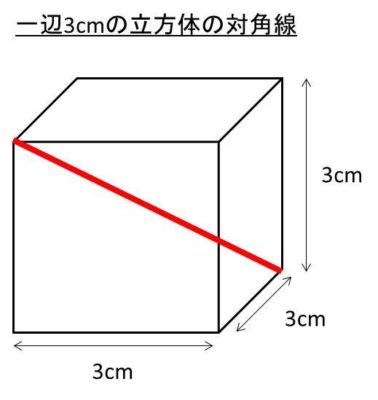
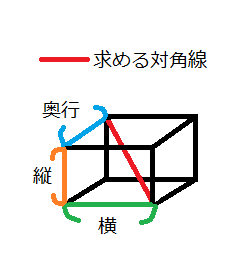
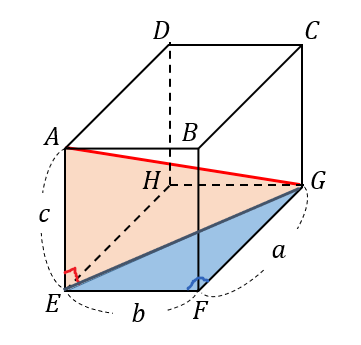
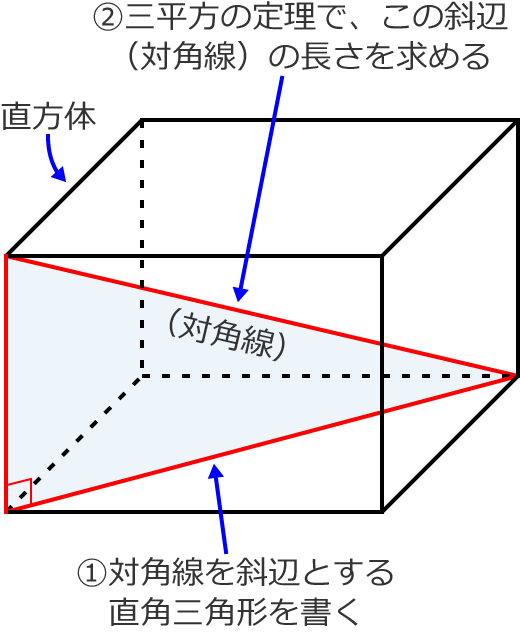
31/1/ 直方体、立方体の対角線の長さを求める考え方 直方体、立方体の対角線を求めるには、 次のように2つの三角形に分けるて考えていきます。 すると、赤い直角三角形に注目すると 求めたい対角線 の長さは次のように表すことができます。 でも、ここで の長さって何? ? となって困ってしまいます。 なので、次に底面を半分にした青い三角形に注目します。 次の問いに答えなさい。① 1つの対角線の長さが8cmの立方体の表面積は何㎠ですか。② 表面積が216㎠の立方体の体積は何㎤ですか。③ 底面が1辺10cmの立方体の容器に水を540㎤入れると、水の深さは何cmになりますか。よって、 \(AP\) の長さは、立方体の対角線 \(AG\) の \(\displaystyle \frac{3}{32}\) です。 \(1\) 辺が \(4cm\) の立方体の対角線の長さは \(4\sqrt{3}\) なので \(AP=4\sqrt{3}×\displaystyle \frac{3}{32}=\displaystyle \frac{12\sqrt{3}}{5}\)
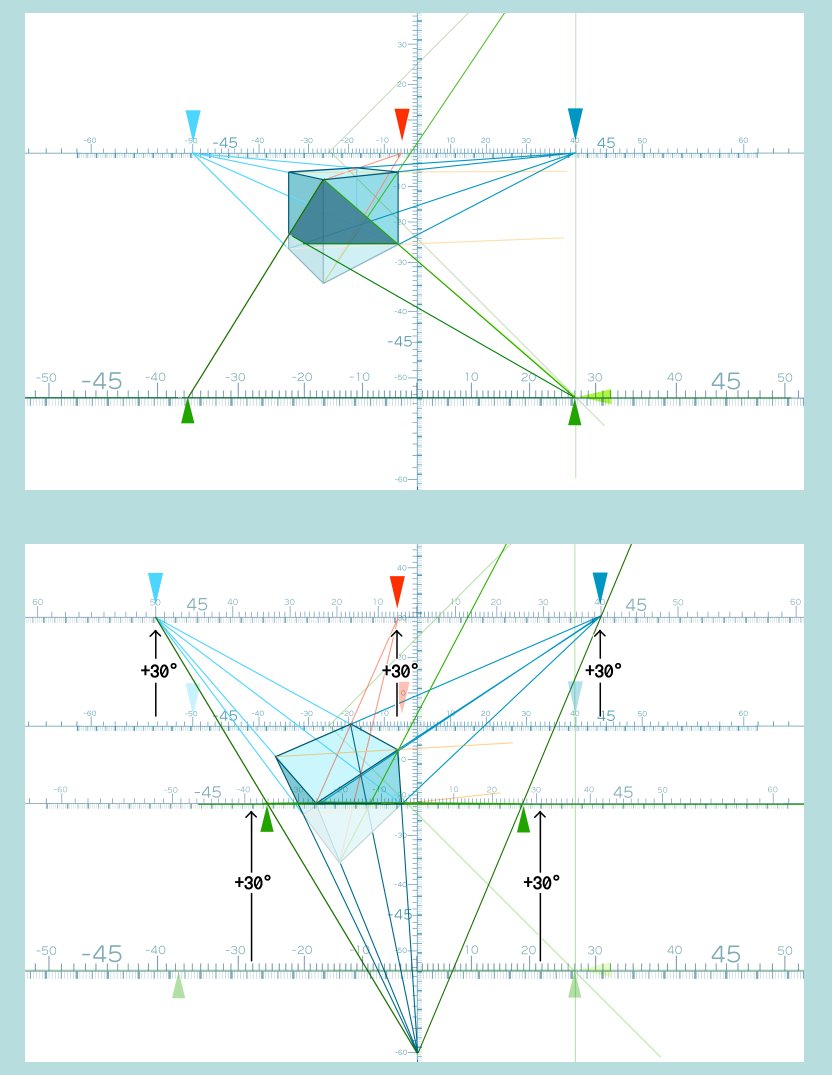
赤井さしみ 立方体の片方の対角線を通る切断面を回転させる という操作を考えるとこうなるような気がします 回転後の角度が悪くて見づらいですが
立方体の対角線 角度
立方体の対角線 角度-QI814 円柱が滑らないためには μ が大きい方がいいだろうし、転倒するには a が小さくて b が大きい方がいいはずだから、答えは ④ とすぐにわかります。 選択肢問題だからこのようにして解けばいいのですが、一応ちゃんと説明してみます。 物体が滑る対角線 BD B D の長さは、 ∴ ∴ 対角線 BD= √a2 b2 B D = a 2 b 2 ① となります。 このように、長方形の対角線の長さは、対角線を斜辺とする直角三角形を書いて、その直角三角形に三平方の定理を使うと求めることができます。 長方形の対角線の長さの
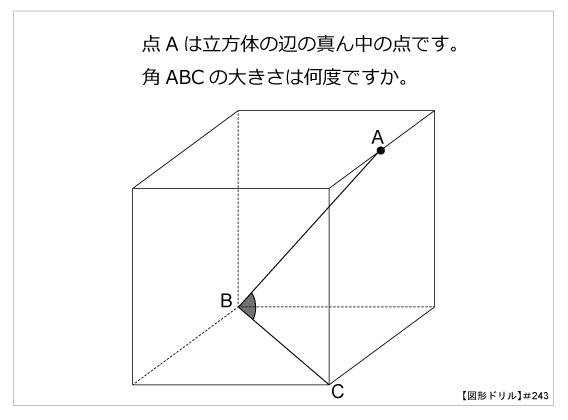



図形ドリル 第243問 立方体にできる角度 算数星人のweb問題集 中学受験算数の問題に挑戦
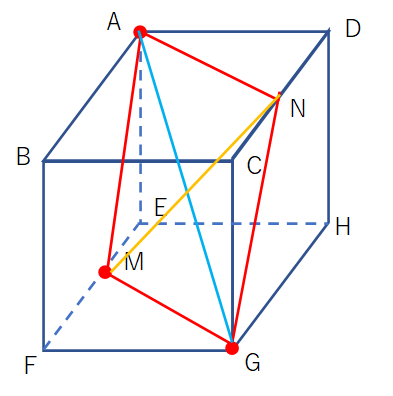
14/2/18 立方体の8個の頂点からうまく4つを選ぶと正四面体になる。 立方体abcdefghのabcdの対角線acとefghの対角線fhをとります。(acとfhはねじれの位置)この 4頂点a,c,f,hを頂点とする立体が正四面体 になります。 これを使って体積を計算すると次のようになります一辺がaの立方体の中にある 一辺が の正四面体を考える. 対角線ABの長さは 対角線BGの長さは ∠AOB=1095°を正四面体角という. ∠EOB=547°をマジック角 という. 直角三角形EOBを考えると、 正四面体角 ∠AOB=2×∠EOB=1095°=109°28' 2a G(1,1,1) x y z 2a 3a θm θm 547o11/5/19 立方体の対角線の長さ=√(√2a^2 a^2)と求めることができるわけです。 具体的に計算していくと、立方体の対角線の長さ=√(2a^2 a^2)=√3a と求められます。
ここで使うのが「 (★)」の内容。 直角二等辺三角形は「90°、45°、45°」の角を持つ。 90°は直角であり、直線BEと直線FEは直角はなしていない。 したがって、 直線BEと直線FEのなす角は45°であり、 直線BEと直線GHのなす角は、90°である・・・(答)回転角度2ˇ=nの回転をn回繰り返すことによって元に重なる場合をn回回転対称と呼びCn と記す。 C2 C3 C4 C6 図5 格子の対称性(点群) 図6 は。、回転操作以外の、鏡面操作˙、回転と鏡面操作を組み合わせた回映操作Sn = ˙ Cn を示して いる。化学辞典 第2版 立方晶系の用語解説 結晶の単位格子が立方体となる結晶系.直交する3本の結晶軸a,b,cが互いに等価であるため,等軸晶系とよぶこともある.結晶の点群の対称要素としては,3軸が同等なため,立方体の各体対角線方向に対して互いに109°28′の角度をなして交わる4本
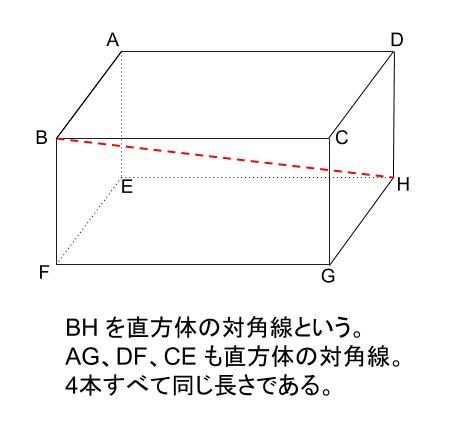
直方体の対角線 立体にも対角線という言葉を用います。 直方体の対角線とは、下図のような 内部を貫く線分のことです。 直方体の対角線の長さ たて、横、高さがそれぞれ、\(a,b,c\) である直方体の対角線の長さを \(L1/5/ Rで球面幾何学正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。 その一方で(原蹠と対蹠を結ぶ経路に注目する)球面幾何学側からのアプローチでは「正四面体を二枚張り合わせた立体」が出発点となります。直方体の対角線の長さ これ無しでは生きていけない身体に! 手持ちの三脚がコインロッカーに入るか、事前に確認したくて対角線を算出しました。 ありがとうございました。 アウトドアでタープを張る際の、ロープの長さを計算しました。 手持ちのロープでは長さが足りませんでした。 正しくコートのラインを引くのに役立ちました! すごい! 駅のコイン



Http Www Ikushin Co Jp Shuppan Textimg 17matokan Chuhyo Sugaku Hon Pdf
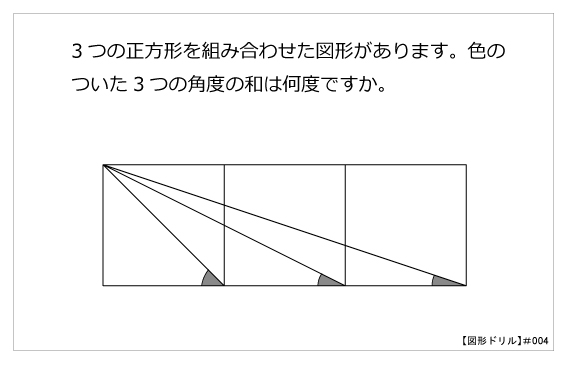



図形ドリル 第4問 正方形の角度 算数星人のweb問題集 中学受験算数の問題に挑戦
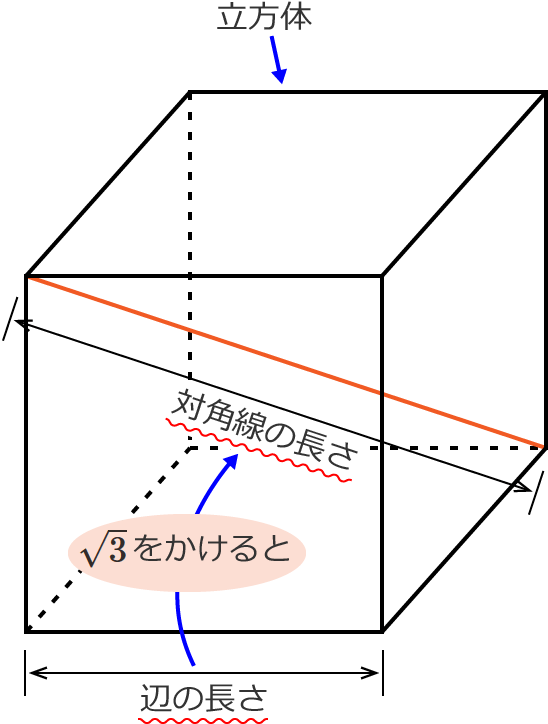
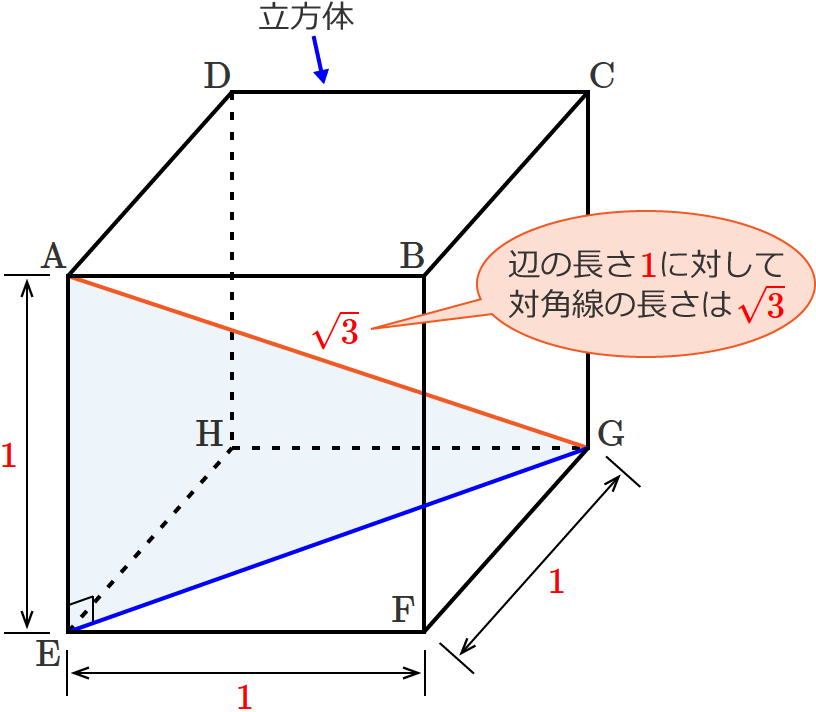
6 角度 sample b ⑷ (佐賀) ⑸ (佐賀) ⑴ 下の直方体の対角線bhの長さ ( 新潟) ⑵ 下の立方体の体積 ( 8 右の図のように,1辺が6cmの立方体abcdefgh直方体、立方体の対角線の長さは公式でラクラク計算できるぞ! 三平方の定理 128 中学数学正八角形の面積を三平方の定理で求める方法を解説! 立方体の1辺の長さをaとすると、 √3 a で対角線の長さが求められるんだ。 つまり、 立方体の辺の長さに「√3」をかけるだけでいいんだ。 たとえば、1辺の長さが4cmの立方体があったとしよう。 すると、この対角線の長さは、 4√3 になるってわけ。




立方体を対角線まわりに1回転させてできる回転体の体積 数学の偏差値を上げて合格を目指す
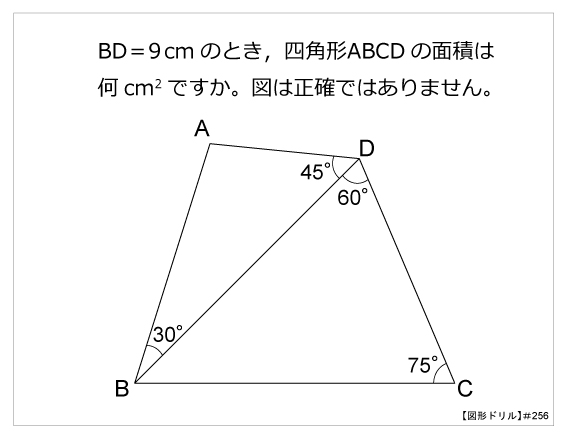



図形ドリル 第256問 四角形と対角線 算数星人のweb問題集 中学受験算数の問題に挑戦
の3回回転(回反)軸は立方体の体 対角線と平行にする 立方 三方晶系では3 回回転軸は単純単位 格子の体対角線方向に沿ってとり、 a=b=c、α=β=γ≠90ºとする Z軸は常に唯一の回あるいは6回 回転(回反)軸と平行にとる.X、Y軸 はZ軸と90ºに、また互いに1ºにな5/8/09 立方の対角線が辺となす角度θ求め方を教えてください。お願いします。「立方」って何や、立方体かいな。「方向余弦」を検索してみると吉。三辺 a,b,c の直方体の対角線が辺 a と成す角の cos は、a / √(a~2b~2c~2) です。a=b=c ならば無料授業動画サイト「StudyDoctor」 http//studydoctorjp/家庭教師テキスト http//studydoctorjp/?page_id=4英語はmiki先生 https//www



立方体の切断についてこの画像の立方体の切断面の角度は 90度 Yahoo 知恵袋




直方体と立方体の対角線 無料で使える中学学習プリント
直方体と立方体の対角線 直 方 体 の 対 角 線 の 長 さ a b c a2+b2+c2= 2 立 方 体 の 対 角 線 の 長 さ a a a a2+a2+a2= 2 2 6 3 2 2+62+3 = 2 4+36+9= 2 49= 2 7= 3 3 3 32+32+3 2= 9+9+9= 2 27= 2 27 = A G 2 4 3 A 4 2 3 5 2+4 = 2 25+16= 2 41= 2 41 = 3 2 6 A B A 3 2 3 6 62+= 2 36+64= 2 100= 2 10=入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺三角形 直角二等辺三角形 21年 立体の切断 15年 図形の移動 共通部分 大阪 面積の和 12年 13年 3年生 ジュニア23/6/19 対角線の長さとなす角で表された四角形の面積 対角線の交点をEとする { }${AE=a,\ BE=b,\ CE=c,\ DE=d}\ とおくと p=ac,\ q=bd$ また,\ 角度は0 正四面体の計量:表面積・2面のなす角・高さ・体積・内接球の半径・外接球の半径と立方体



オイラーの多面体定理と正多面体 正方形における平方対角線 Square Diagonal と立方体における立方対角線 Cubic Diagonal の関係について Qiita




立方体を対角線まわりに1回転させてできる回転体の体積 数学の偏差値を上げて合格を目指す
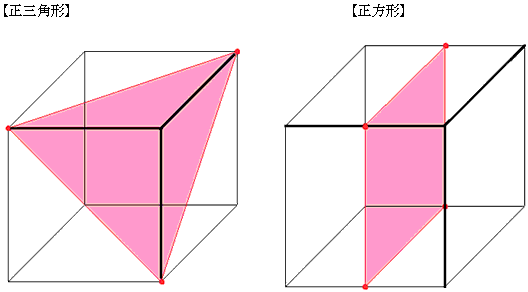
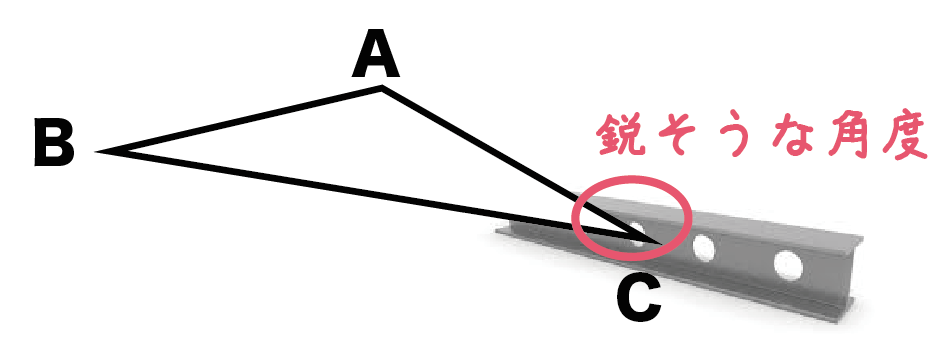
立方体の辺の長さに √3 3 をかける と求められます。 なので、例えば、辺の長さが a a の立方体の場合には、 対角線の長さは、 対角線の長さ = = 辺の長さ ×√3 × 3 = a×√3 = a × 3 = √3a = 3 a ∴ ∴ 対角線の長さ = √3a = 3 a となります。 また、辺の長さが 10 10 の立方体の場合には、 対角線の長さ(1)対角線への垂線の長さ (2)三角形への垂線の長さ 参考 両方を 表示 一辺の長さが1の立方体abcd efgh がある。 (1)頂点eから対角線agへ下ろした垂線の長さを求めよ。 (2)頂点eから afhへ下ろした垂線の長さを求めよ。 頂点eから下ろした立方体の対角線の角度を求める問題 今日は、立方体の対角線の角度を求める問題を紹介します。 適性検査でも出題されそうな面白い問題なので、親子で挑戦してみてください! 図1の立方体で、2つの面の対角線 (2本の赤線)の交わる角度を求めなさい。 赤線部分はすべての長さが等しいので、 正三角形 になることがわかります。 60° (答え) 教材のご相談は



中学数学です 立方体で面bdeと対角線agの交点がmです Agの長さ Yahoo 知恵袋



立方体における ひし形の面積の求め方を教えてください 以下の条件で対角 Yahoo 知恵袋
答 正三角形 ※ ちなみに, \angle \rm AFC は正三角形の内角なので 60^\circ です これを立方体の真上から見下ろすと, \angle \rm ABC に重なって見えるため 90^\circ に見えます しかしこれはあくまで見かけの角度であって, 本当の角度は 60^\circ です このように実際の角度と異なって見えるのは, 正三角形に対して 「斜めの方向」 から見ているからです立方体の描き方 この節では1点透視図における立方体の描き方を説明します。 以下の2種が代表的な作図法です。 距離点(左右いずれかの45°消失点)を利用する作図法です。 D点法とも呼ばれます。 作図がとにかく簡単であり、目立った欠点もないため立方体の各面とのなす角(楕円角度)は いずれ もcos1(√2/√3)=約35度 であるなお等 測投影図を√3/√2「=約122倍 に拡大し,軸



立方体の対角線の計算方法 白丸くん




オイラーの多面体定理と正多面体 正方形における平方対角線 Square Diagonal と立方体における立方対角線 Cubic Diagonal の関係について Qiita
2点透視図法(45°)で描いた立方体(青線)を元に、3点透視図法に変換する。 Aとb、Cとbを結び対角線Ab、Cbを引く。 a から任意の角度で斜線を引き、Abとの交点 E を求める。 V1 から E を通る線を延長し、との交点 F を求める。 V2とも結び、Gを求めます。



重なった球と立方体 本郷中学 2009年 パズル おもしろ算数問題



Metatronic Metalogue 5 121




直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ



白い立方体の数はいくつ 第8回算数オリンピック トライアル問題より 中学受験ー算数解き方ポータル




問題174 立方体に潜む正多角形
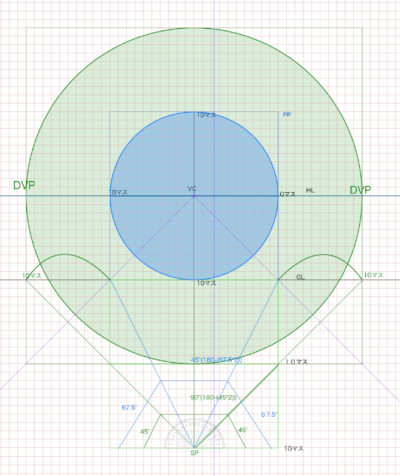



パースにおける視円錐とは何か 画角は何度にするべきか 対角線の消失点とは何か
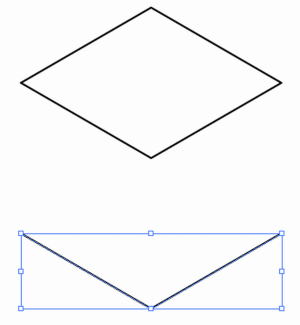



立方体の穴 テクニカルイラストレーターの
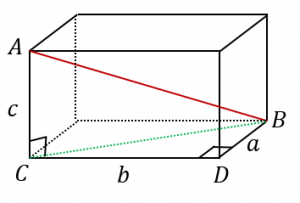



立方体と直方体の対角線の長さ 具体例で学ぶ数学




高校数学a 2直線のなす角 例題編 映像授業のtry It トライイット
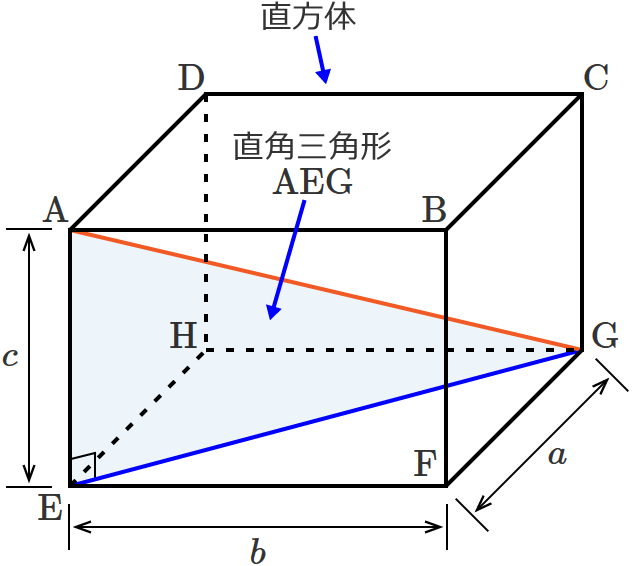



直方体の対角線の長さの求め方




中学数学 空間図形



立方体の対角線の計算方法 白丸くん



3
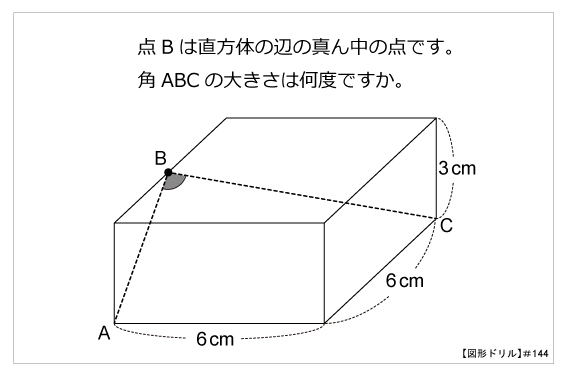



図形ドリル 第144問 直方体の角度 算数星人のweb問題集 中学受験算数の問題に挑戦




正方形 Wikipedia




Cube Taraognn
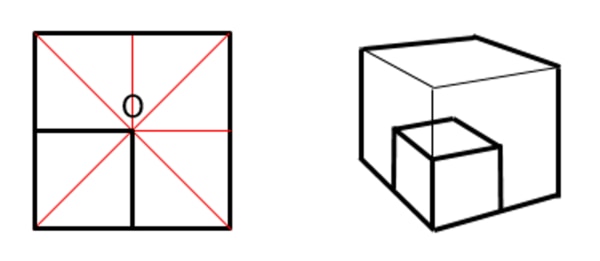



技術者のためのイラストレーション講座 基礎編 4 株式会社アイデア
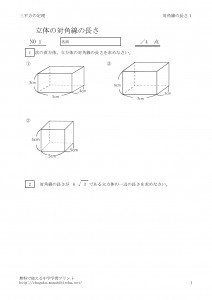



直方体と立方体の対角線 無料で使える中学学習プリント



立方体の切断 楽しいクイズの発信基地 クイズ大陸




入試の問題がわからないです 数学の授業がないので教えて頂けると助かります Clear




立方体を対角線まわりに1回転させてできる回転体の体積 数学の偏差値を上げて合格を目指す




赤井さしみ 立方体の片方の対角線を通る切断面を回転させる という操作を考えるとこうなるような気がします 回転後の角度が悪くて見づらいですが




超立方体 Wikipedia




立方体を対角線まわりに1回転させてできる回転体の体積 数学の偏差値を上げて合格を目指す



中学数学 直方体の対角線 中学数学の無料オンライン学習サイトchu Su




角cafの大きさを教えてください 1辺が3の立方体です 私は角cab 45 その他 学校 勉強 教えて Goo
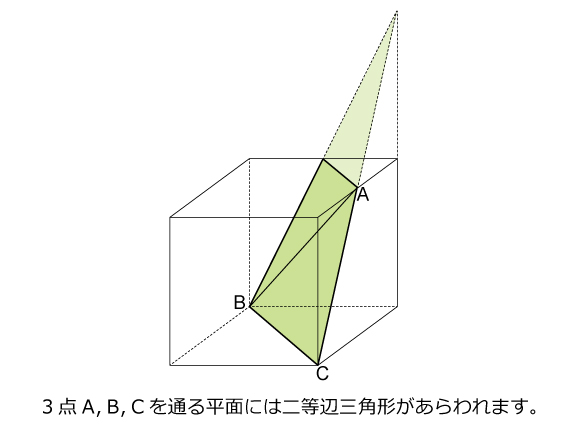



図形ドリル 第243問 立方体にできる角度 算数星人のweb問題集 中学受験算数の問題に挑戦
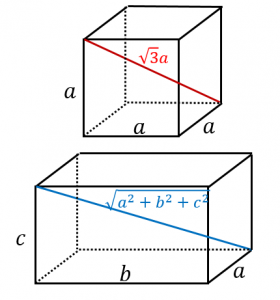



立方体と直方体の対角線の長さ 具体例で学ぶ数学
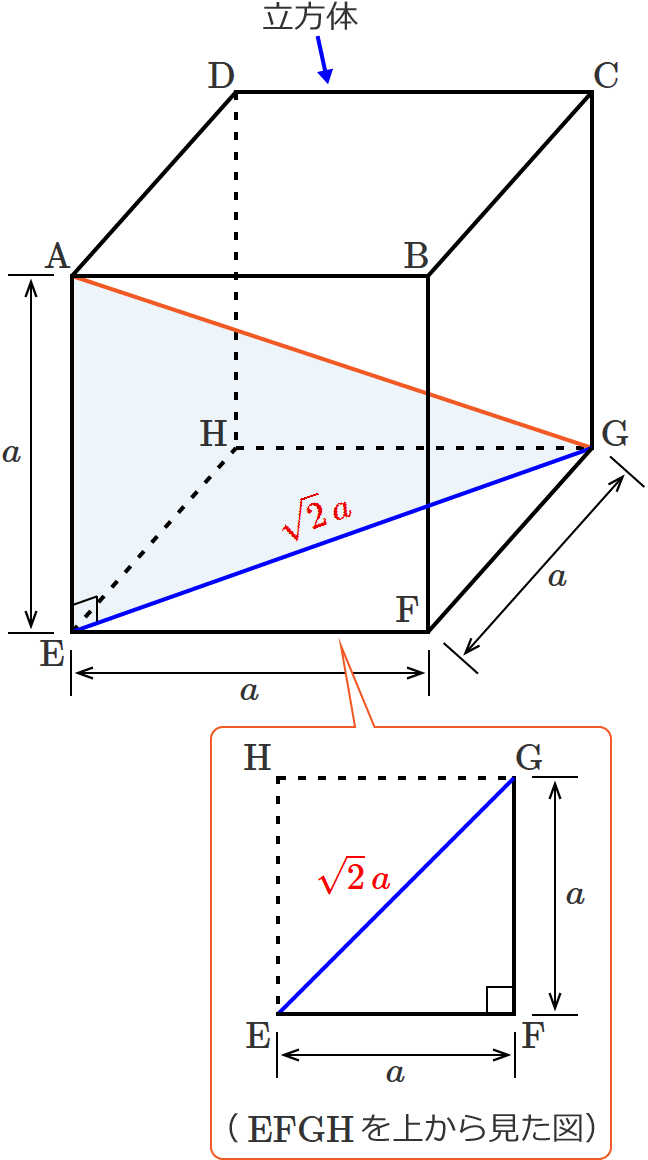



立方体の対角線の長さの求め方



1



立方体の対角線が切断面と交わるときなぜci ie 1 2になるのでしょ Yahoo 知恵袋




立方体の対角線の角度を求める問題 恋する中高一貫校 適性検査 徹底攻略
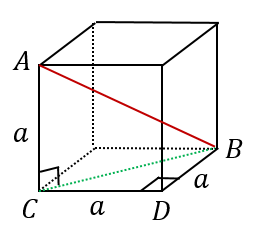



立方体と直方体の対角線の長さ 具体例で学ぶ数学
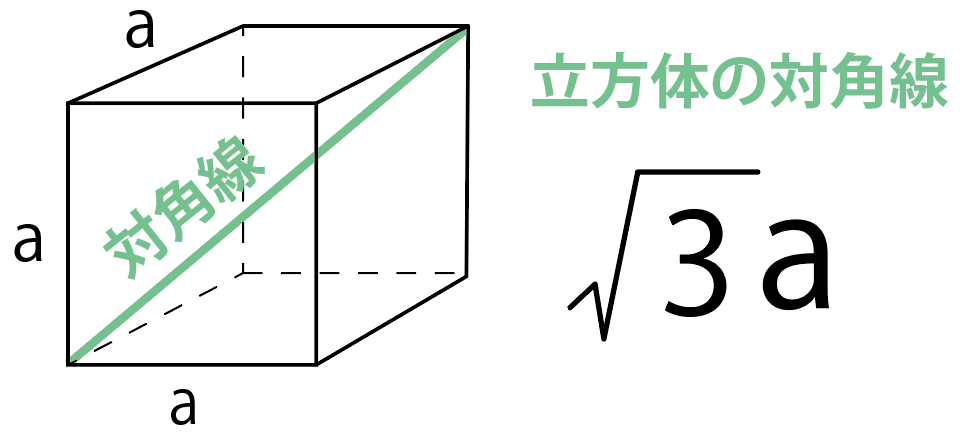



計算公式 立方体の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
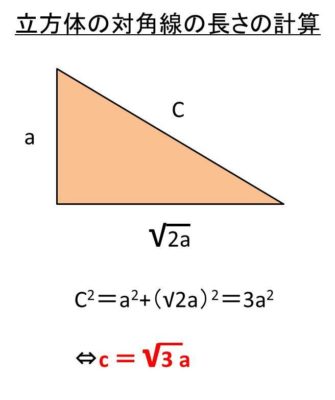



立方体の対角線の計算方法 白丸くん




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



直方体の対角線の長さ 高精度計算サイト




1辺の長さが3である立方体abcd Eeghの対角線ceに頂点aから垂線akを下ろす Clear



消失点の角度 数学 パースフリークス




立方体を対角線まわりに1回転させてできる回転体の体積 数学の偏差値を上げて合格を目指す



立体切断の切り口 これひし形なの 長方形かと思った の解き方について 算田数太郎の中学受験ブログ




高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月



1




計算公式 直方体の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




直方体の対角線の長さの求め方




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり




05 2191号 v溝の加工方法 Astamuse



問題174 立方体に潜む正多角形



計算公式 立方体の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




角cafの大きさを教えてください 1辺が3の立方体です 私は角cab 45 その他 学校 勉強 教えて Goo




イラストレーターで立方体をつくる チロリ
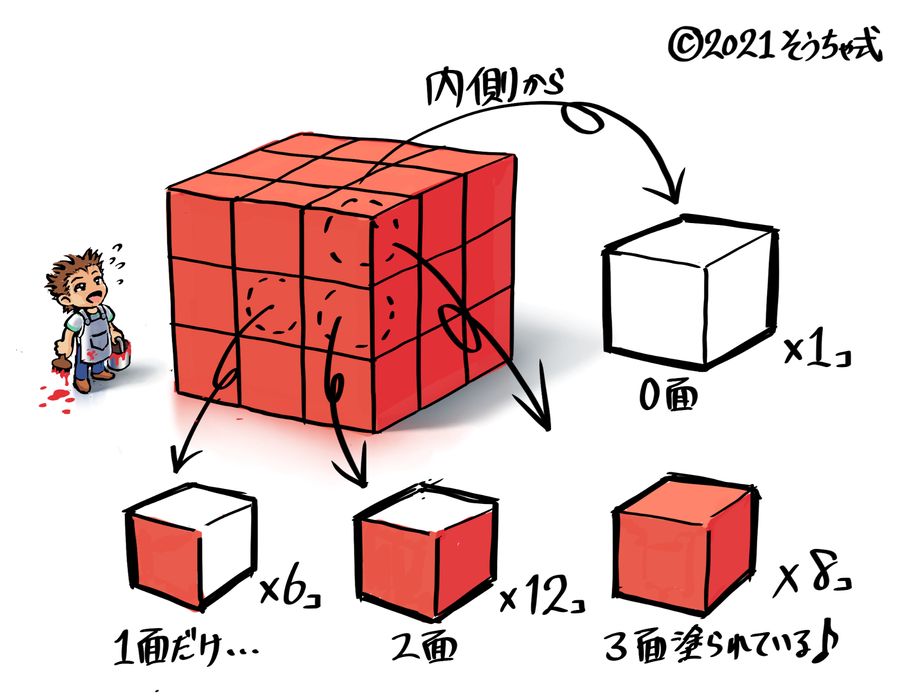



中学受験 直方体 立方体のまとめ 立体図形 そうちゃ式 受験算数 2号館 図形 速さ




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
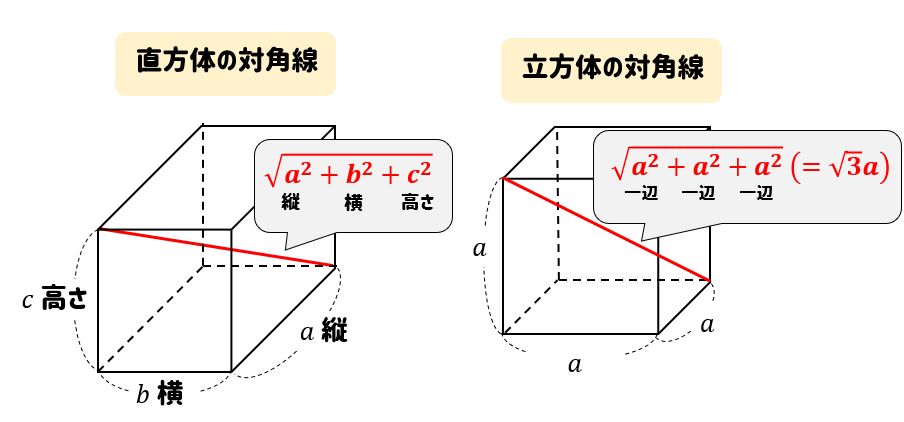



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ



1



一辺の長さが3である立方体abcd Efghの対角線ceに頂点aから Yahoo 知恵袋




質問 数学 立方体での対角線や垂線の長さ オンライン無料塾 ターンナップ
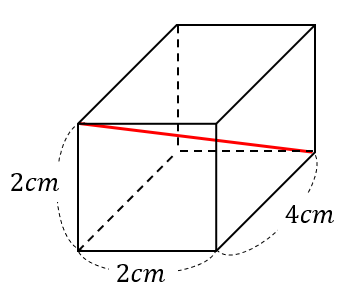



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ
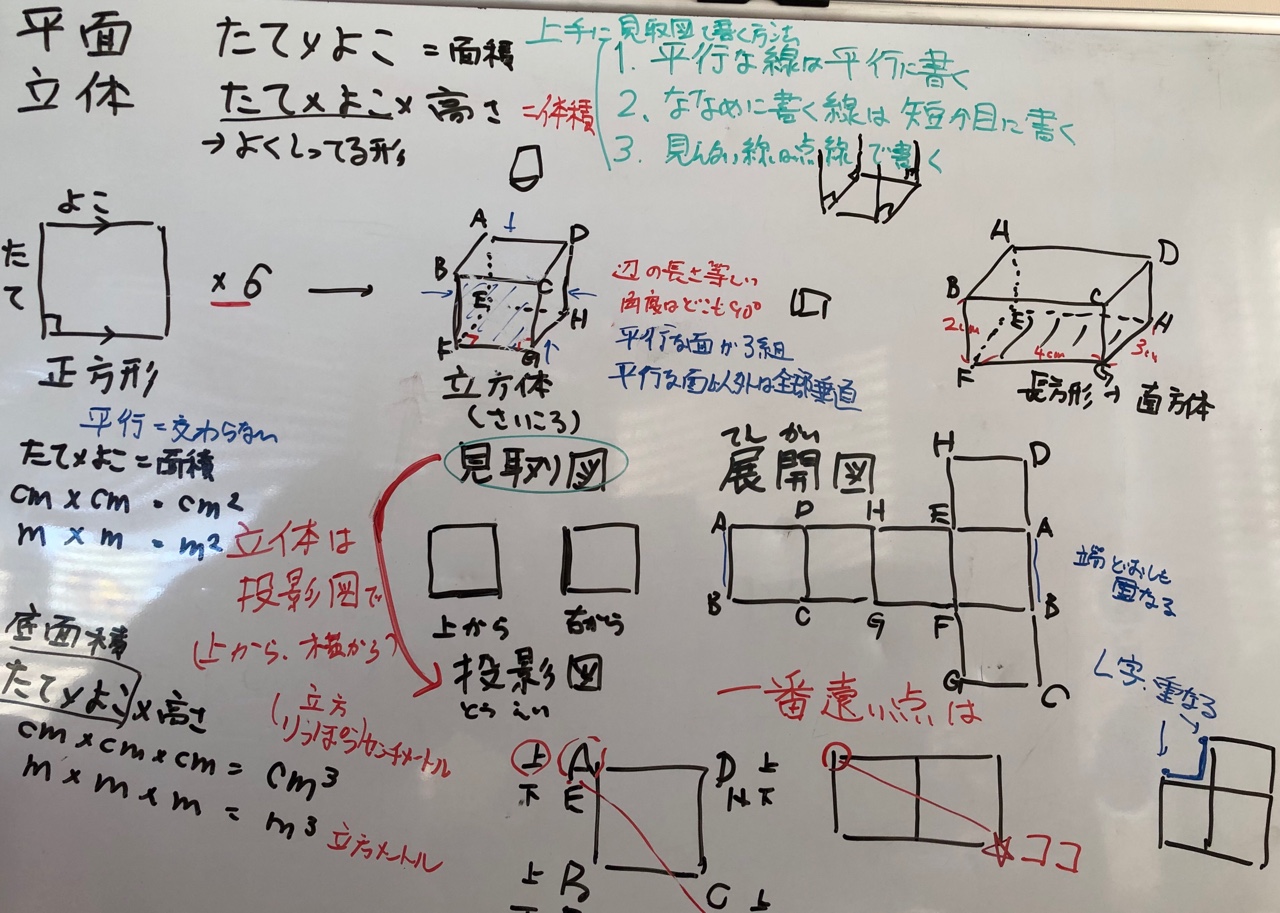



立方体と直方体 塾との進捗ギャップ埋めその1 妹入塾準備




図形ドリル 第243問 立方体にできる角度 算数星人のweb問題集 中学受験算数の問題に挑戦




直方体の対角線の長さの求め方 中学3年数学 Youtube
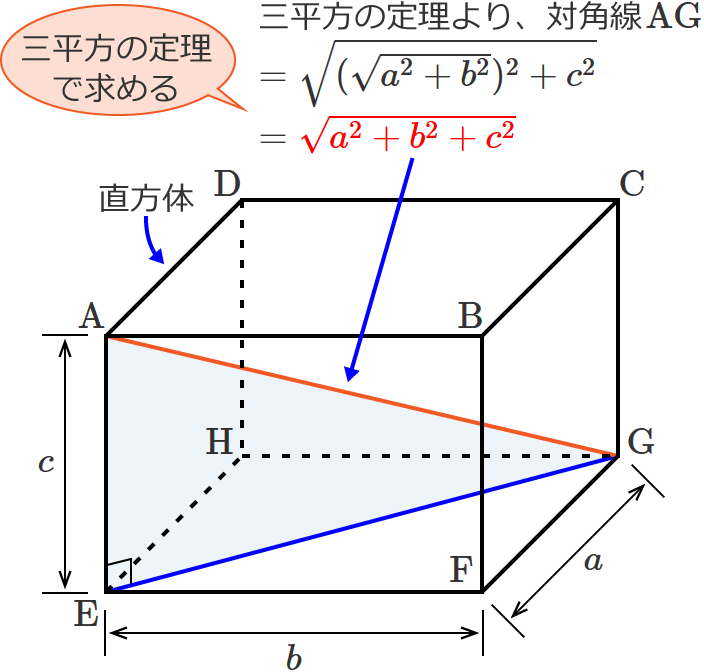



直方体の対角線の長さの求め方




四角形の4辺の長さと対角線のなす角がわかっている時 対角線の長さを 数学 教えて Goo




台形の対角線の求め方 この図のaとcの対角線の求め方を教えて下さい Okwave
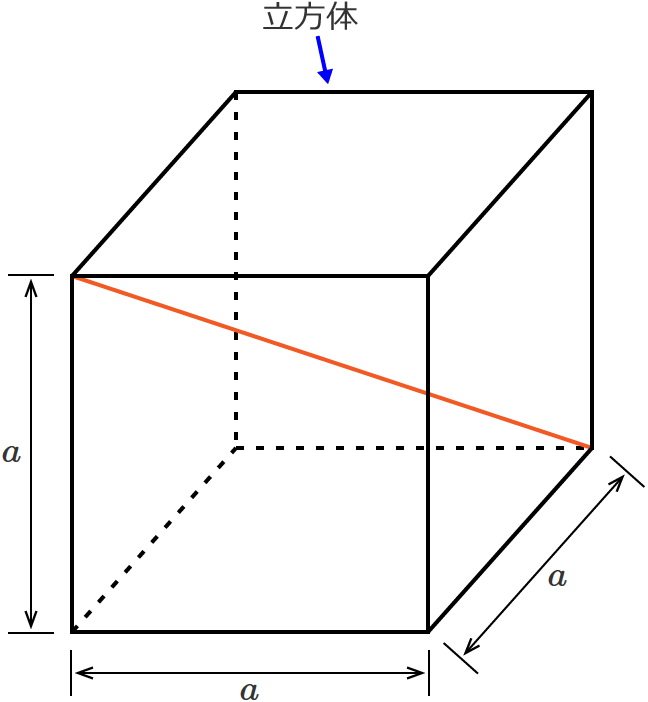



立方体の対角線の長さの求め方



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係




直方体と立方体の対角線 無料で使える中学学習プリント




高校数学a 2直線のなす角 練習編 映像授業のtry It トライイット
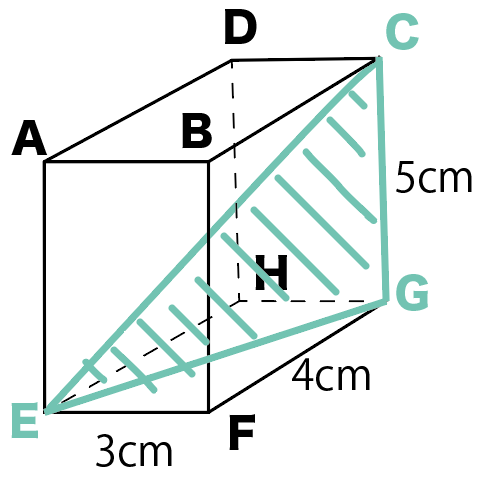



計算公式 直方体の対角線の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
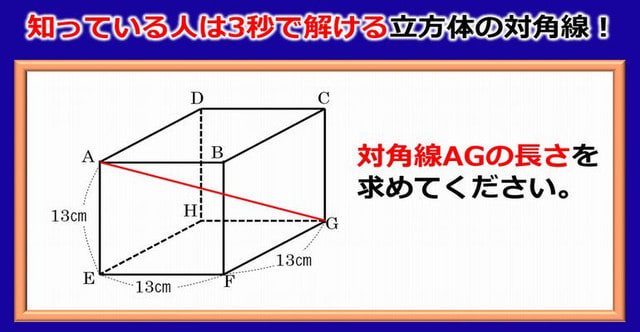



数学の基礎 知っている人は3秒で解ける立方体の対角線 暇つぶしに動画で脳トレ



立方体の対角線の長さの求め方
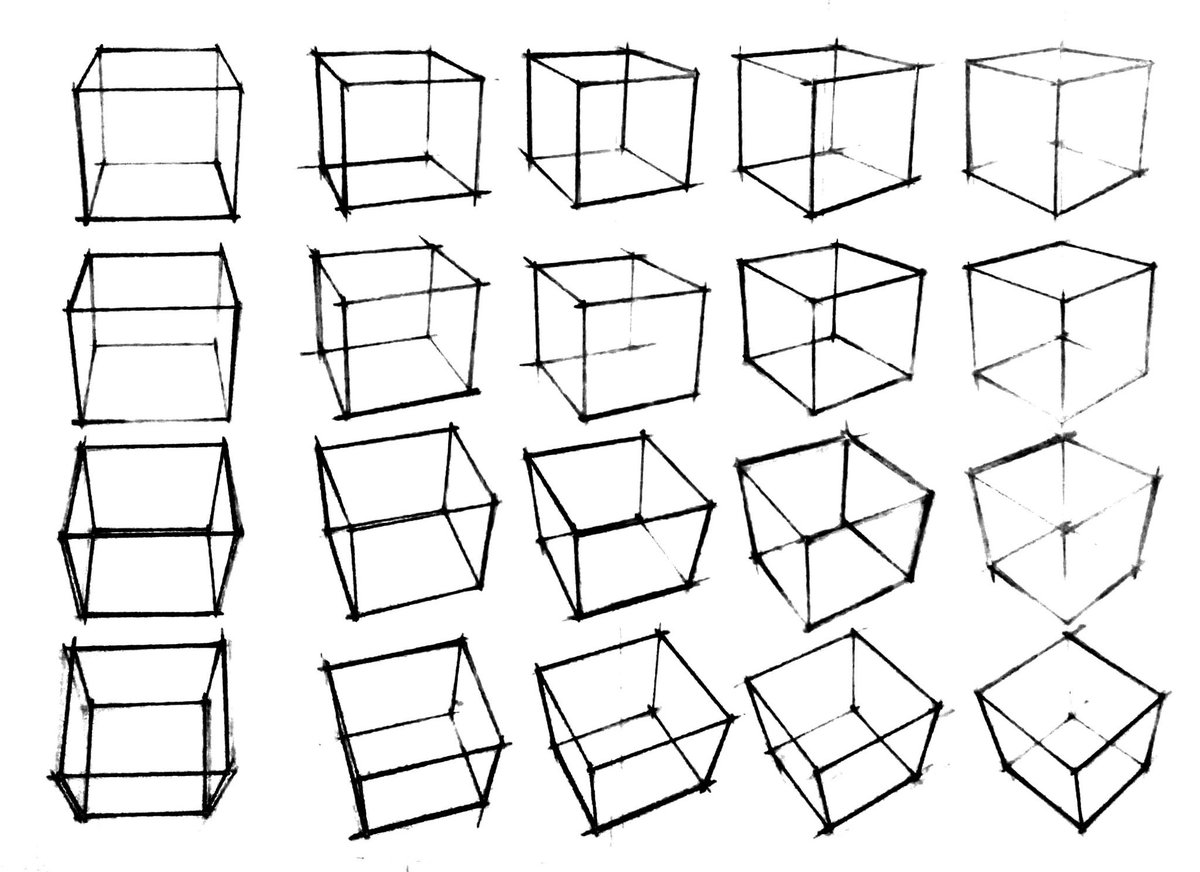



5分だけ描く 立方体の描き方など
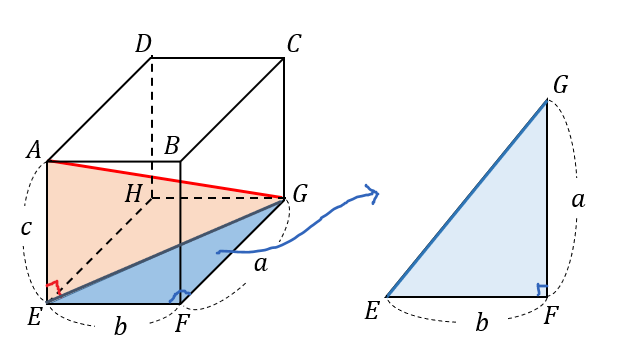



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ



中学校3年生の数学の授業




ルパート王子の立方体 Wikiwand
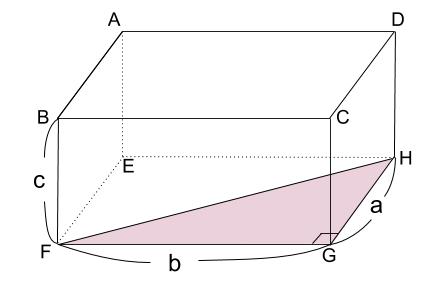



中学数学 直方体の対角線 中学数学の無料オンライン学習サイトchu Su



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係



立方体の対角線が切断面と交わるときなぜci ie 1 2になるのでしょ Yahoo 知恵袋




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり



消失点の角度 数学 パースフリークス




介線法は 立方体しか描けないのでしょうか パースのついた面を対角線を使って増やせば直方体にはなりますが また直方体を描く透視図法はありますか 透視図法 パース
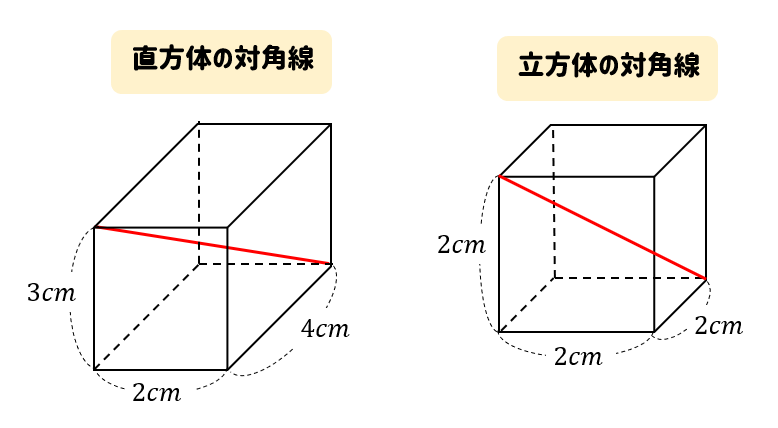



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ
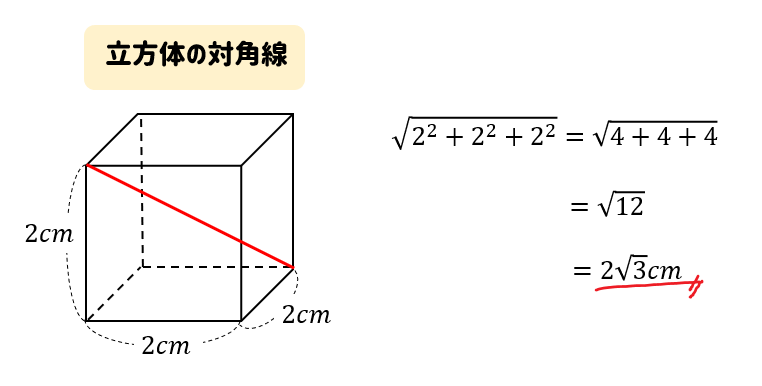



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ
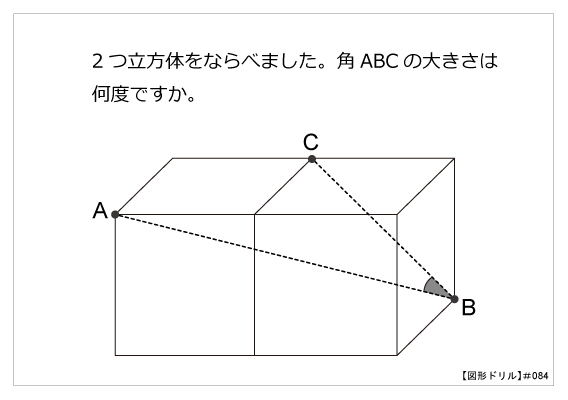



図形ドリル 第84問 立体にできる角度 算数星人のweb問題集 中学受験算数の問題に挑戦



対角線のお相手探し 雑学のソムリエ




高校数学 円に内接する四角形の対角線の長さと面積 受験の月
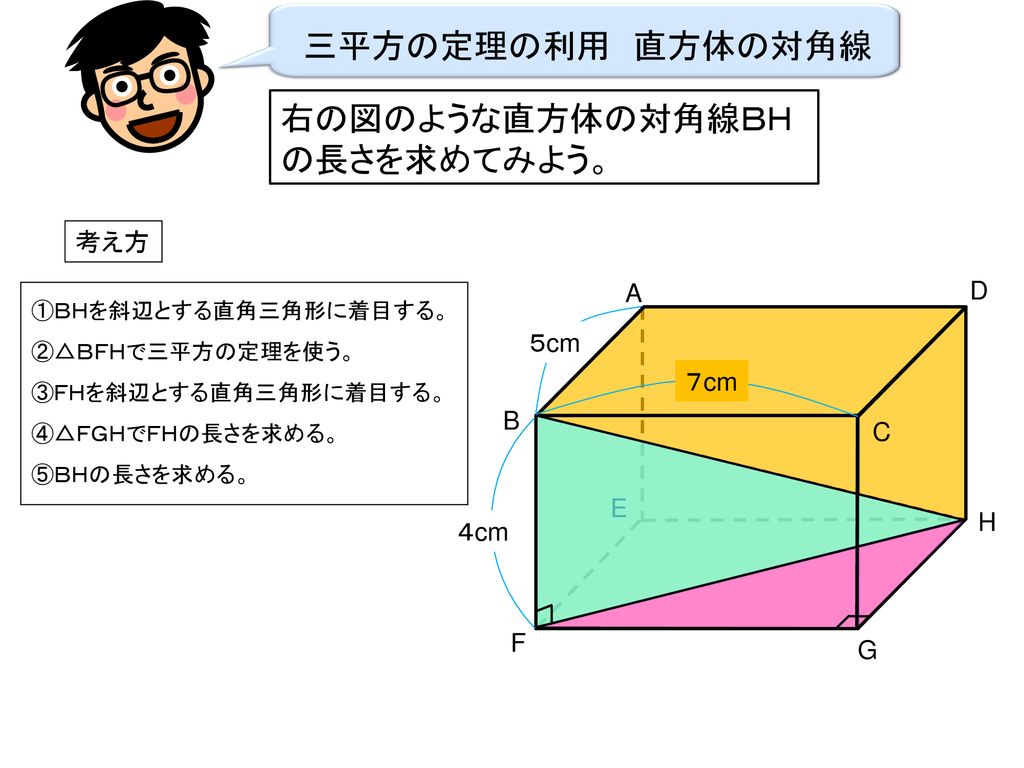



右の図のような直方体の対角線bhの長さを求めてみよう Ppt Download



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ




三角形の辺の比と角度の問題 そらいろ日記 言葉の宝箱



立方体の対角線の長さの求め方



直方体の対角線の長さの求め方



Mathematics 三平方の定理 5 空間図形と三平方の定理 働きアリ The 2nd



0 件のコメント:
コメントを投稿