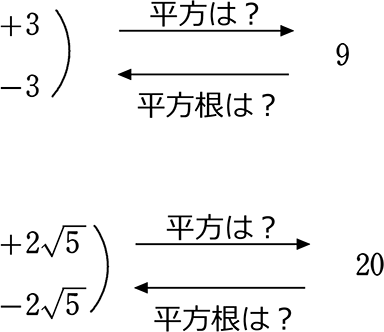
2乗して a になる元の数を a の平方根といいます. 例3 3 2 =9,(3) 2 =9だから, の2つあります. これらはまとめて ±3 で表すことができます. だから, 9の平方根は±3 ともいえます. 例4 5 2 =25,(5) 2 =25だから, の2つあります 平方根って何なの? まず最初に、平方根という聞いたこともない単語。 平方根とはある数字のことなんですが、 カンタンに言うと、2乗(同じ数を2回かける)したらできる数字のことです。 たとえば、2は4の平方根になります。 3は9の平方根になります。 4は16の平方根になります。 41 平方根(1) 设图中的小方格的边长为1,你能分别说出两个长方形的对角线ab、 a′b′的长吗? 由勾股定理可知 ab²=12²+5²=169, ab=13 a′b′ ²=1²+2²=5, 那么a′b′ =? 猜猜看? 创设情境 一般地,如果一个数的平方等于a,那么这个数叫做a的平方根

世界一わかりやすい数学問題集中3 2章 平方根
4の平方根 根号
4の平方根 根号-立方根性质 编辑 语音 (1)在 实数 范围内,任何实数的立方根只有一个 (2)在实数范围内,负数不能开平方,但可以开立方。 (3)0的立方根是0 (4)立方和开立方运算,互为逆运算。 (5)在复数范围内,任何非0的数都有且仅有3个立方根(一实根,二"平方" 通常是写成一个小小的 2: 意思是 "4 的平方等于 16" (小的 2 代表数在乘法里出现了 2 次)



平方根ってなに 意味や求め方を超分かりやすく解説 1日目 ベントー
平方根 √ 、立方根 3√ 、累乗根 n√ を計算します。 2乗するとaになる数x、つまりはx²=aを満たす数xのことをaの平方根というので、正の数aについての平方根は√xと-√xの2つが存在します。 (負の数は2乗すると正の数になるので) これらを合わせて±√xと書いたりします。 今回は1/4の平方根ですが、2乗して0 の平方根は 0 のみであり、平方根が一意に定まるのはこのときに限られる。 単位長と任意の長さ a が与えられたとき、 a の正の平方根の長さは定規とコンパスを用いて作図することができる。 定義 数 a に対して、 x 2 = a を満たす x を a の平方根という。
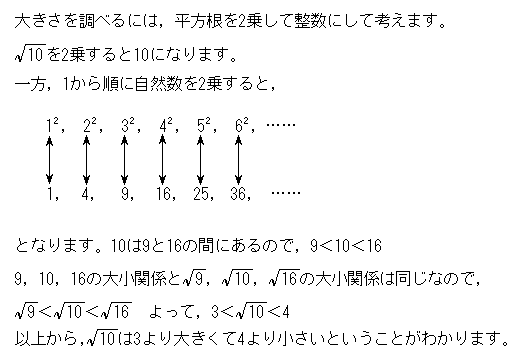
かずお式中学数学ノート11 中3 式の展開と因数分解・平方根 著者の高橋一雄先生が「かずお式中学数学ノート11」(朝日学生新聞社刊)をテキストにして、ビデオ講義をしています。 内容は式の計算を扱っています。 テキストさえ購入していただければ1414 は何の平方根ですか? 立方根 下で √ の前についている 3 は立方根の 3 である。 3√2 = the cube root of two 3√3 = the cube root of three 3√4 = the cube root of four 3√27 = 3 The cube root of 27 is three それ以上 The fourth root of eightyone is three 81 の 4 乗根は 3 である。なので、「 \(2\) の正の平方根」は \(14\) よりも大きくて \(15\) よりも小さいことが分かりますね。 実は、「 \(2\) の正の平方根」は \(\cdots\) と無限につづく数であることが分かっています。 ちょうど、円周率がと無限に続いていくのと同じように。
こうして平方根が求まる理由を考えると,次の桁を求める段階で次の計算をおこなってい ることがわかる.すなわち,xに対してy2 xとなるyまで求まっているとき,2yが左に, x−y2 が右に得られている.次の桁はzとしてもとめるが,それは(2yz)z x−y2 となる 出来るだけ大きなzになるよう1桁分 の平方根はそのうえの数字の「521」だよ。 やったね。 13ステップは長すぎるぜ^^ まとめ:筆算をつかった平方根の求め方は辛い 平方根の求め方に筆算をつかうと、 でかい数の平方根を求めるとき; 第3章 平方根 1 平方根 0 はじめに 皆さんこんにちは。新章突入です。これから学習する内容は、その名もズバリ『平方根』です。 『平方根って何?』と思う人も『ルート』とう言葉は聞いたことがあるでしょう。それでもピーンと来ない人は、電卓についている謎のボタン『』、 これ



2



1
有一个有趣的方法去计算平方根,并且每次的答案会越来越准: 一、 先做一个 猜测 (我们猜 4 是 10 的平方根) 二、 除以 猜测 (10/4 = 25) 三、 加上 猜测 (4 25 = 65)比如,求4的平方根,可以先求出4的平方根,4的平方根是2和2,则4的平方根是2i和2i。 注:在虚数里规定i²=1 延伸:相关概念 1、负数 比0小的数叫做负数,负数与正数表示意义相反的量。平方根計算法 実行結果 正整数 12の平方根の整数部 = 3 正整数 1234の平方根の整数部 = 35 正整数 の平方根の整数部 = 351 正整数 の平方根の整数部 = 3513 ok 改良 1234の平方根を求める。 1234を2桁ずつに分ける。 ①12の平方根を求める。 0 < 12 135 < 12 < 1357




中学数学 平方根 のコツ 平方根とは 平方根の大小



数学の平方根の問題で写真の事なんですが 答えが 9分の4と Yahoo 知恵袋
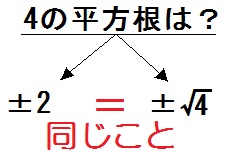
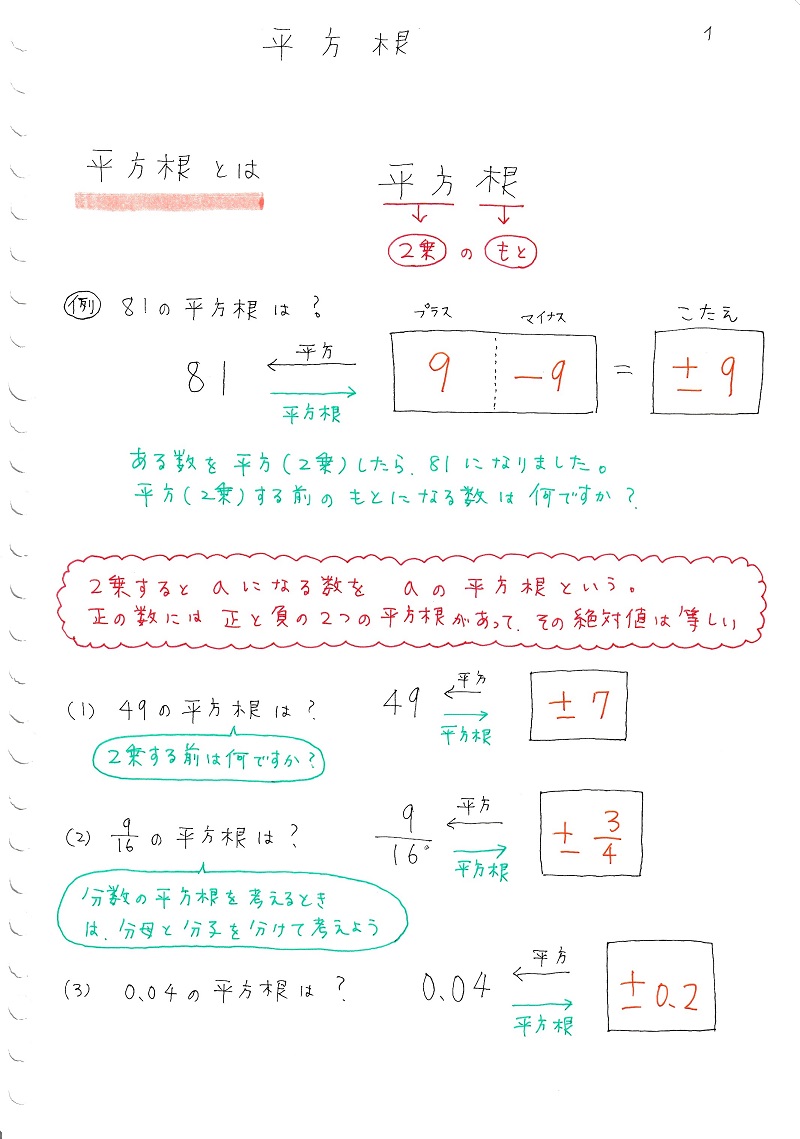
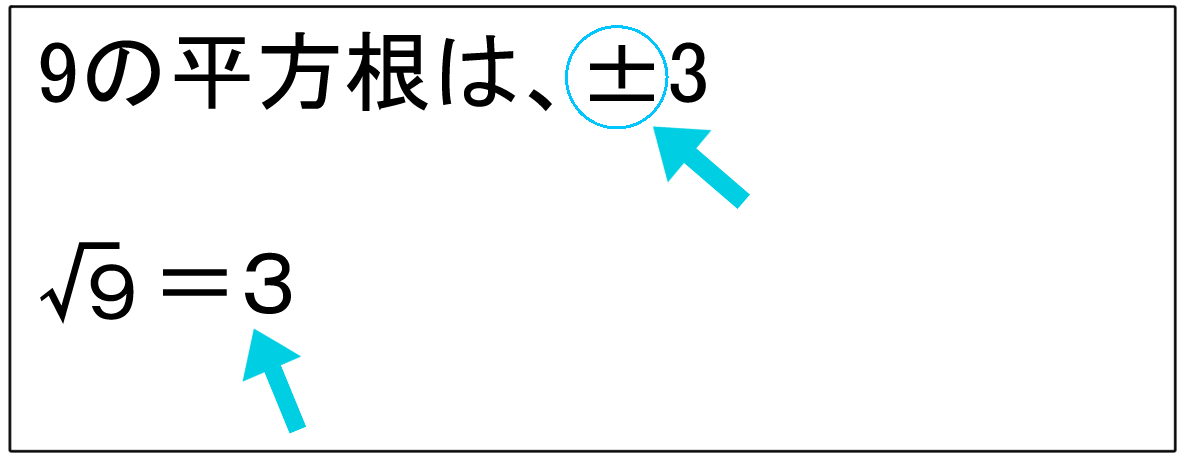
平方根の計算についてです。 ab=3√5、bc=3√5の時、次の式の値を求めよ。 a^2b^2c^2abbcca 解答は画像の様になっていました。平方根や累乗根を数式で表す場合は、ルート( )という記号を使います。 9の平方根を表す場合は、 9 と書きます。 9の平方根は3なので「 9 =3 」となります。 累乗根を表す場合は、ルートの前に小さい数を置くことで何乗根かを表します。 2を2乗すると4になります(→2は4の平方根)。また、−2も2乗すると4になります(→ −2も4の平方根)。つまり、4の平方根は2と−2です。正の数の平方根は、このようにと−の2つあります。 〈具体例〉 9の平方根は3と−3 16の平方根は4と−4 25の平方根は5と−5



2



平方根ってなに 意味や求め方を超分かりやすく解説 1日目 ベントー
平方根 平方根とは、2乗する前の数のことです。例えば、 a^2=4 という関係を満たすとき、 a のことを4の平方根と言います。 つまり、4の平方根は、2と ー 2 になります。 では、3の平方根は、何で平方根の足し算と引き算は、 ルートの中身が同じ数を1つにまとめます。 パッと見は中身が異なる場合でも、 ルートの中身を簡単にすると同じになるケースもある ので、ルートの中身を可能な限り簡単にしてから足し算・引き算を行います。 50 18 を計算 平方根 第11講 例題1 問4 平方根と乗法公式 問題はこちら 解説は下にあります。 "平方根 第11講 例題1 問4 平方根と乗法公式" の 続きを読む




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




世界一わかりやすい数学問題集中3 2章 平方根
共 81 个结果 下载 精品 2份 41 平方根帮课堂2122学年八年级数学上册同步精品讲义(苏科版) 21 江苏 教案 专辑 帮课堂2122学年八年级数学上册同步精品讲义(苏科版) 11 全等图形帮课堂2122学年八年级数学上册同步精品讲义4 は4の平方根のうち正の数を表す。 つまり 4 = 2
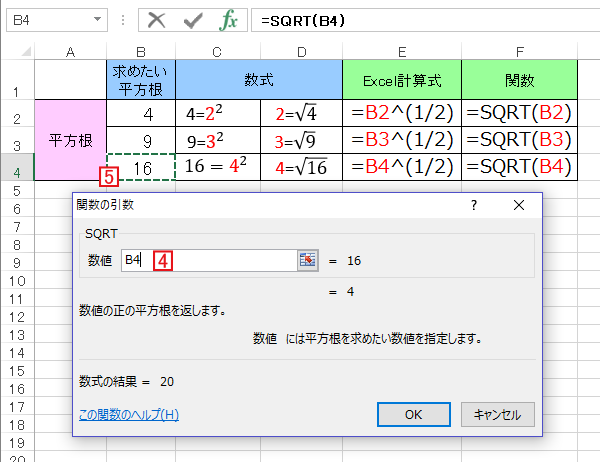



べき乗 Nのm乗 平方根 ルート 立方根を利用 Excel エクセル の使い方




平方根とは すうがくのいえ




4の平方根やルートは 9 16 25 36 49の平方根とルートは 平方根とルートの違い 意味 や計算方法を解説 プラスマイナス More E Life




数学 中3 16 平方根 Youtube




平方根とは すうがくのいえ
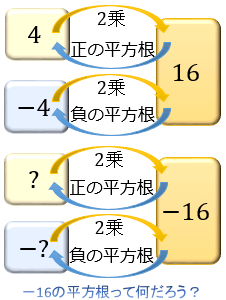



平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




16 の平方根は と聞かれたら 2 です では Clear




70以上 5 の 平方根 シモネタ




高校数学i 3 4 平方根の性質 Youtube




中学数学3年 平方根とその近似値 大小 有理数と無理数 受験の月




平方根 2乗するとaになる数 教遊者
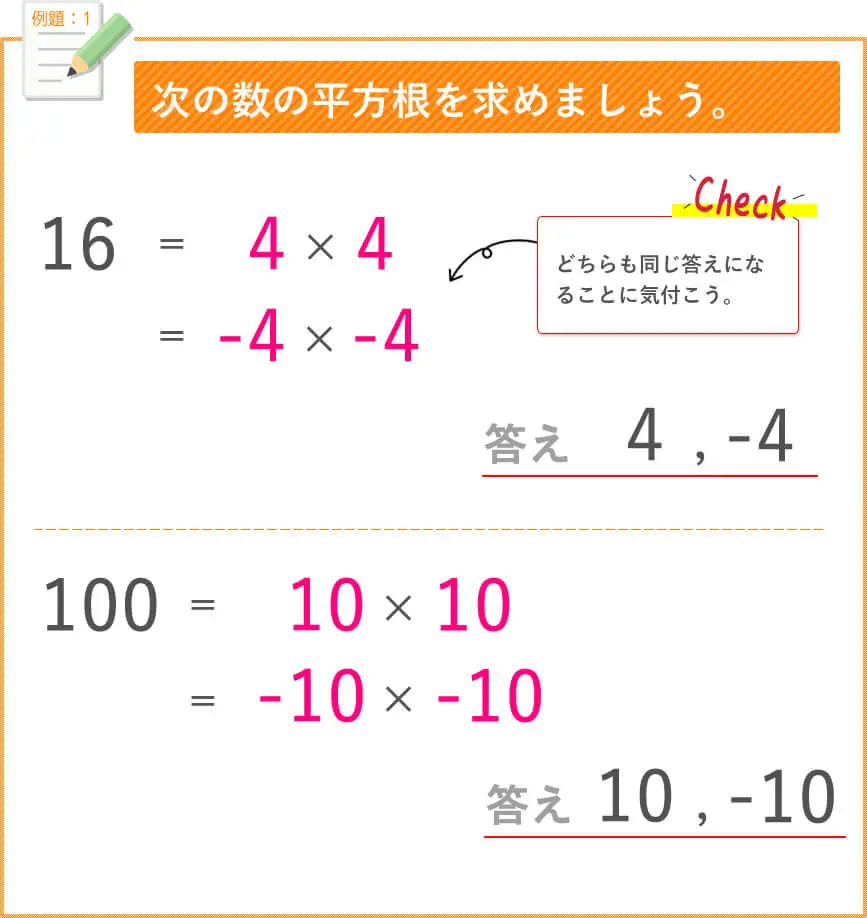



実数 平方根とルート 平方根とルートの基本を理解しておこうの巻 Vol 4 3回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の 看護学校 看護予備校



平方根ってなに 意味や求め方を超分かりやすく解説 1日目 ベントー




平方根1 Youtube




平方根とは すうがくのいえ




1学期に習う中3数学その4 平方根について 中3 数学 家庭教師とっしゅ先生の授業 小学生 中学生




平方根とは さわやか さくらぐみ




二次方程式の解き方 平方根を利用 チーム エン




平方根とルート 根号 の概念 有理数と無理数の違い リョースケ大学



25分の4の平方根の解き方を教えてください 25分の4 4 2 Yahoo 知恵袋



4の平方根は2 というのは間違いと参考書に書いてありますが どうしてでしょ Yahoo 知恵袋



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




無料 中3数学 基本解説 解答プリント 309 平方根1 意味




高認数学 第1回 式の計算



平方根の筆算のしかた




平方根 2 ルートと平方根の違い バカでもわかる 中学数学



2乗 平方根




Tossランド 平方根 の暗記プリント Dl可




2の平方根 Wikipedia
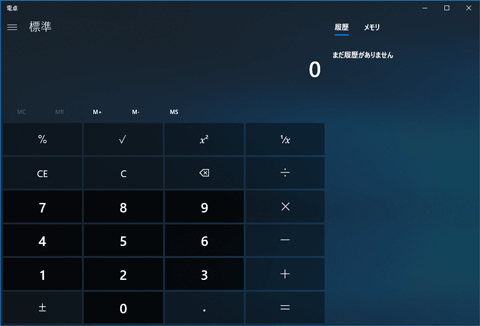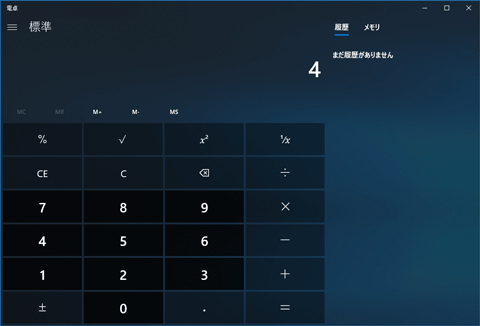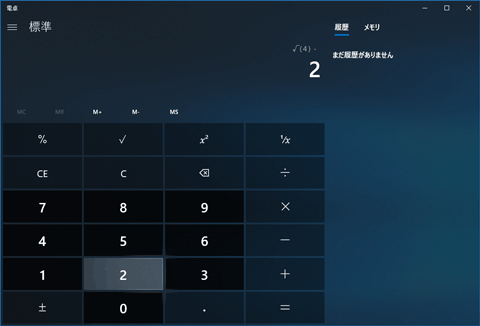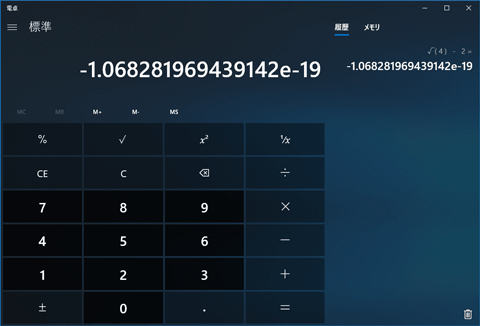



Windowsの標準電卓で4の平方根が2でなかった仕様がようやく修正 Pc Watch




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月




平方根とは サイエンスの人気 最新記事を集めました はてな
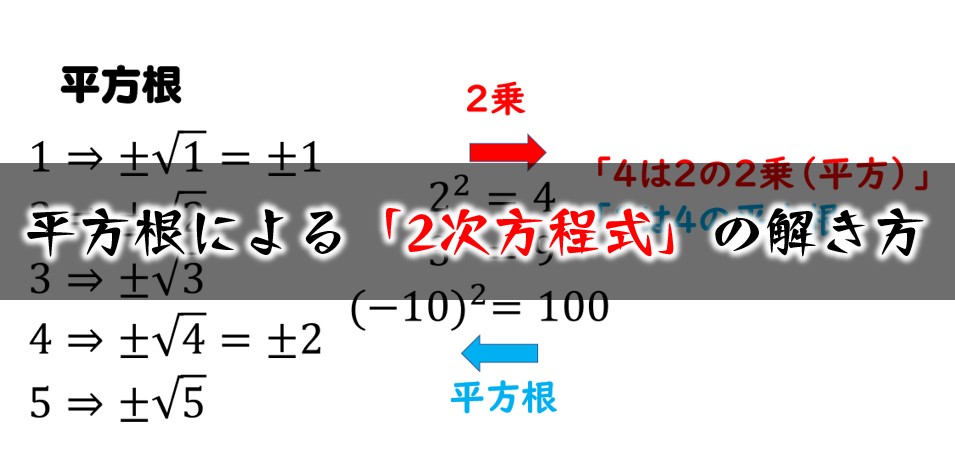



2次方程式の解き方 平方根を利用 数学fun



Http Www Gunma Ct Ac Jp Staff Nakajima Lecture Math1b E7 Ac Ac10 E5 9b 9e E6 95 B0b E5 B9 E6 96 B9 E6 A0 B9 Pdf




平方根 ルート64 8 ではない の意味がわかりません 中学数学 定期テスト対策サイト




平方根 とは 根号の意味や性質 値の求め方について 数学fun



1



中学数学 平方根
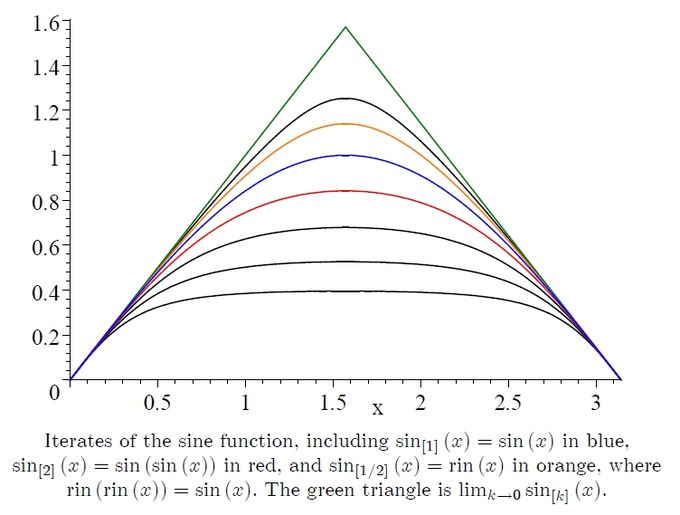



函数的平方根 Wikipedia




タクミ 数学テクニック Sur Twitter 平方根 ルートの2乗は絶対値 T Co D30aykq1sc



1



5の平方根は ルート5ですか また ルートの中に5を入れると Yahoo 知恵袋
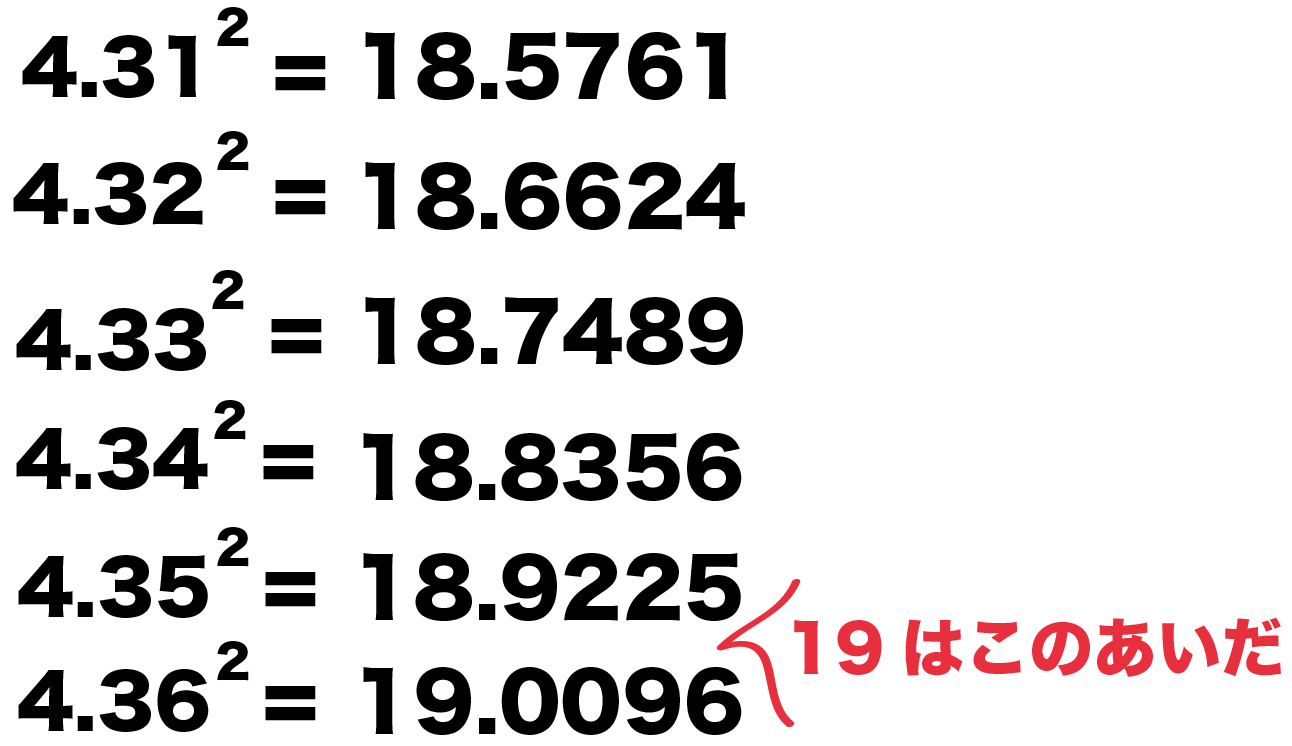



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




数と式 平方根について 日々是鍛錬 ひびこれたんれん



2



中学数学 平方根 のコツ 平方根とは 平方根の大小




中3 数学 平方根の利用 についてです 問題 大きい円の中に 半径5c 数学 教えて Goo



中学数学 平方根 ママ塾ノート




平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく




なぜ 4なんでしょうか 誰か回答をお願いします Clear




2の平方根 デザインtシャツ通販 Tシャツトリニティ




Square 4 Sqrtdfrac3649 Descubre Como Resolverlo En Qanda



平方根ってなに 意味や求め方を超分かりやすく解説 1日目 ベントー




平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




2の平方根 Wikipedia




平方根 とは 根号の意味や性質 値の求め方について 数学fun




基礎から学ぶ 平方根 の計算 ふらっつのメモ帳




中3の平方根の初歩的な問題です Clear




中学数学 平方根 のコツ 平方根とは 平方根の大小



平方根 2 ルートと平方根の違い バカでもわかる 中学数学




平方根 とは 根号の意味や性質 値の求め方について 数学fun




要点 平方根とは Youtube




ルートとは 平方根の求め方を解説 Youtube




これで完璧 平方根の基礎 中3数学 中学生の勉強法




田村 良輔 あぶない計算 平方根 正の平方根 ルート 根号 ルート4 2 ルート9 3 ルート25 5 Kyon2 キョンキョン 小泉今日子 キョン は シカ科 しゃぶしゃぶ 麻薬




数と式 平方根について 日々是鍛錬 ひびこれたんれん



平方根って何だろう 理数系無料オンライン学習 Kori



平方根 ルート10はどのくらいの大きさ 中学数学 定期テスト対策サイト




数と式 平方根について 日々是鍛錬 ひびこれたんれん




無料 中3数学 標準問題 問題プリント 312 平方根4 乗法 除法2



平方根 1 基本のルール バカでもわかる 中学数学



1




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




2 Sqrt016 Descubre Como Resolverlo En Qanda




中3数学 平方根とは 練習編 映像授業のtry It トライイット




平方根とは すうがくのいえ




02 号 平方根の逆数計算方法 計算回路 及びプログラム Astamuse




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




鬼の平方根演習プリント 1 4の授業 数学 受験ブログ




北辰テスト対策 数学 平方根 蒼進塾 そうしんじゅく さいたま市 真剣に努力する姿勢を育む




二次方程式の解き方1 チーム エン




Vba 数値の絶対値を返す Abs関数 平方根を返す Sqr関数



数学 根号を含む計算 平方根など 数学



4分の1の平方根は 1 ーなのですが 21ーではない Yahoo 知恵袋




1 2乗って何 どうしてそれがルート 平方根 になるのか 数学の面白いこと 役に立つことをまとめたサイト



Http Yonominami J Saitama City Ed Jp Subj Suugaku Subj Math 3002 Pdf




平方根とは さわやか さくらぐみ




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ
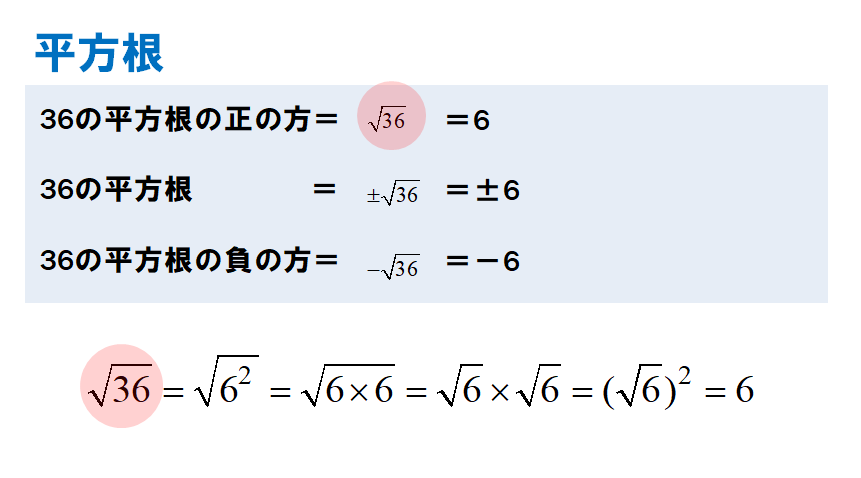



中3数学 平方根の性質の定期テスト対策問題 Examee




平方根の考えを使った解き方 教遊者




学習指示 中3 数学 平方根 P37 P39 坂東市進学塾 スタディ ポート 港日記 楽天ブログ




平方根 1 基本のルール バカでもわかる 中学数学




コミック 数学サバイブ物語 平方根 暇人たちの遺したもの 端野 洋子 ブルーバックス 講談社 1 6
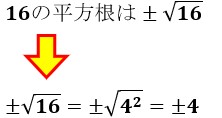



基礎から学ぶ 平方根 の計算 ふらっつのメモ帳



平方根の筆算のしかた




正の平方根ってなんですか 笑 よく分からないです 教えてくれる方いたら嬉しいです Clear



0 件のコメント:
コメントを投稿